I don't own a temperature control option, is there a way that we can work around this?
Long story short, temperature has a huge impact on viscosity. 
Water for instance is a good example to think of. When it gets colder, it starts to freeze and when it gets warmer, it starts to slowly boil. Applying that concept, each fluid has it's own characteristics and can display variations at different temperatures including temporary or permanent alteration of the sample. It is highly advised to explore your sample by using a actual temperature control option. If you are working with a RheoSense viscometer, contact us to learn more about temperature capabilities.
Interested in seeing data and analysis on temperature dependent viscosity values? We have a number of technical resources that you can access:
- Thermosensitive Polymers as Pharmaceutical Excipients
- Can Your Proteins Take the Heat?
- Can Your Proteins Take the Heat II?
- Automated Viscosity Screening Through Temperature Sweeps
As you are exploring temperature control options, there is also a temperature model that can be applied without a temperature control. NOTE: THIS WILL ONLY APPLY TO NEWTONIAN SAMPLES. If you do not know if your sample is Newtonian then stop immediately and figure out that part first. The way to figure out if your sample is Newtonian or non-Newtonian is to run at various shear rates. If you need guidance on this, please contact us at info@rheosense.com
Your sample is Newtonian? Then we use an “Arrhenius-like” Equation to model the viscosity of a fluid with a change in temperature, as shown in the equation before. Typically, as temperature goes up, viscosity will go down.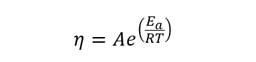
η = Viscosity
R = Gas constant
Ea = Arrhenius activation energy
A = Pre-exponential factor
T = Temperature (ambient or measured temperature in °C)
It is like the same Arrhenius equation used to model the rate of a chemical reaction, except the absence of a negative sign to cause viscosity to lower with increasing temperature. When written in logarithmic terms, the equation looks like this:
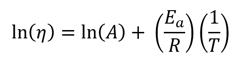
If the fluid tested obeys this equation, then a plot of the viscosity versus reciprocal absolute temperature (aka Kelvins) should be linear. Here, ln(A) is the intercept of this plot (b), Ea/R is the slope(m), and 1/T is x. When substituted, this equation is formed:
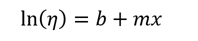
To get viscosity, the exponential is added back into the equation:
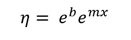
This is then converted into our final equation:
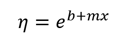
If you have any questions on using this model or expanding your measurement capabilities to include temperature, feel free to contact us!
Written by: Grace Baek, RheoSense Operations Manager
COMMENTS