Modeling non-Newtonian Fluids

Analyzing data accurately is vital for decision making throughout the research and development process. Many fluids in the world exhibit non-Newtonian behavior, meaning their viscosity is dependent on shear rate. I remember taking fluid dynamics in college and graduate school and the professor would derive all the equations assuming Newtonian behavior to make our calculations, homework, and tests easier. After graduating, I find that knowing how to measure, correct, and analyze non-Newtonian rheological data is vital when characterizing formulations. And this skill is critical across multiple fields. Real life is complicated!

Scientists have been studying non-Newtonian fluid behavior for decades and have developed models to facilitate characterization. The outputs of these models can be used to interpolate and extrapolate data, categorize materials based on model parameters, and help with computational fluid dynamics simulations. Two commonly used models for pseudoplastic non-Newtonian fluids are the Cross and the Carreau-Yasuda models.

The Cross model is an empirical equation that is used to fit non-Newtonian data (Cross, 1979). More specifically, this model “describes pseudoplastic flow with asymptotic viscosities at zero (n₀) and infinite () shear rates, and no yield stress” (Hackley and Ferraris, 2001). The Cross model can describe many types of fluids including dispersions, polymer melts, and polymeric solutions. Because it is an empirical equation, the model may or may not be appropriate for your application. Meaning, it may not fit your data perfectly. The only way to know for sure is to fit your data with the Cross model and then fit the same data to another model, such as the Carreau-Yasuda model, and compare the results.

The Carreau-Yasuda model is another empirical equation used to fit non-Newtonian data (Bird et al., 1987). Like the Cross model, this model also “describes pseudoplastic flow with asymptotic viscosities at zero (₀) and infinite () shear rates, and with no yield stress” (Hackley and Ferraris, 2001). It has more parameters than the Cross model and is the generalized form of the power law fluid model. The Carreau-Yasuda model is well suited for fluids that are beginning to shear thin, and can be used to describe emulsions, biopolymer solutions, protein solutions, polymer melts, and polymeric solutions.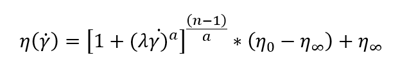

Before applying the Cross model or the Carreau-Yasuda model, you must make sure that your non-Newtonian data has been corrected. If your viscometer or rheometer induces an inhomogeneous flow on your fluid, then you must perform a correction. One commonly used correction is the Weissenberg-Rabinowitsch-Mooney (WRM) correction, which is an analysis method that can determine the “true shear rate,” using the “apparent shear rate” measured by the viscometer (Macosko, 1994).

Model fitting is important across multiple fields and enhances your data analysis. You can use the constants generated by these fits to make decisions and perform calculations relevant for your samples. For example, calculating and understanding the injection force of a therapeutic protein formulation is an important application for the biopharmaceutical industry. Both the Cross and the Carreau-Yasuda models can be used to estimate the injection force of a shear thinning protein solution. When performing non-Newtonian computational fluid dynamics simulations, you can use the model output parameters in the simulations.

Want to learn more about modeling non-Newtonian behavior? Download our new application note for a detailed walk through how to fit non-Newtonian data to both models using the Solver add-in of Microsoft Excel.

Written by: Dr. Zachary Imam, RheoSense Research Scientist

Reference

• M. Cross, Relation between viscoelasticity and shear thinning behavior in liquids, Rheol. Acta, 1979, 18, 609-614.
• B. Bird, R. C. Armstrong, and O. Hassager, Dynamics of Polymeric Liquids: Volume 1 Fluid Mechanics, John Wiley & Sons, 1987.
• Macosko, C.W. 1994 Rheology: Principles, Measurements and Applications. Wiley-VCH
• Vincent A. Hackley, Chiara F. Ferraris, Special Publication 946, National Institute of Standards and Technology, U.S. Department of Commerce, January 2001. [NIST]