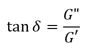In the first installment of our rheology blog series, we defined what Rheology is (branch of physics dealing with the deformation and flow of materials), and shared a few common rheology applications. In our second installation in the series, we defined common rheology terms and concepts. These first two installations set the foundation for this third post, which will dive deeper into rheology concepts as we investigate common rheology equations and model fitting/ corrections.
As was noted in our previous blog, rheology measurements are focused on the rheological properties of materials, including:
- Shear stress τ (mPa): a stress applied parallel to the material cross section on which it acts
- Deformation γ [%]: a change in the dimensions of a body due to an applied external force
- Shear rate γ (1/s): the rate at which progressive shearing deformation is applied to a material
When it comes to rheology measurements there are hundreds of different equations and measurement variations you can take. In this blog, we will be highlighting only the most commonly applied equations.
- Hooke’s Law
- Newton’s Law of Viscosity
- Force
- Moduli Oscillatory Strain
- Moduli Oscillatory Stress
- G’ & G”
- Tan Delta
When measuring deformation of solids, Hooke’s Law of Elasticity is most often applied, relating stress and strain, or more specifically the force (F) needed to extend or compress a spring by some distance (x).
A fluids resistance to flow is typically measured as viscosity. Newton’s Law of Viscosity describes the flow behavior of fluids using a simple linear relation between shear stress [mPa] and shear rate [1/s].
Rheology measures deformation and flow of both solids and liquids, however not all materials are solid OR liquid. Some materials exhibit both viscous and elastic characteristics when undergoing deformation. These materials are referred to as viscoelastic materials. When measuring viscoelastic materials, oscillatory shear flow can be used. Both a strain and a shear rate must be applied when quantifying viscoelasticity. To determine oscillatory shear flow you simultaneously apply a small amplitude oscillatory strain and an oscillatory rate of strain, or shear rate:
Strain:
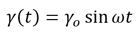
In general, stress will be offset by phase angle :
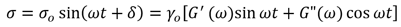
When measuring viscoelastic materials both the elastic modulus (G’) – the elastic behavior of a material when deformed - and the viscous modulus (G”) – the flow of a material when deformed – are measured. It is common to view the relative magnitude of 𝐺" to 𝐺′ as tan delta:
One important thing to note about viscosity (along with other rheological measurements) is that while it is called a measurements, it is not measured, but calculated. Scientists have been studying non-Newtonian fluid behavior for decades and have developed models to facilitate characterization. The outputs of these models can be used to interpolate and extrapolate data, categorize materials based on model parameters, and help with computational fluid dynamics simulations. (Dr. Zachary Imam) Viscosity is dependent on concentration/ volume fraction, temperature, and shear rate. There are models to help model fit all of these different behaviors. Model fitting can support both practical applications (performance predictions and processability) of your measurements and as an investigative tool (complex structure formation, formulation, etc.). A few common model fittings/ corrections used for viscosity measurements are:
- Cross Model
- Carreau-Yasuda Model
- Power Law
- Arrhenius Model
- Intrinsic Viscosity
- Huggins Equation
- Mark-Houwink-Sakurada
- Weissenberg-Rabinowitsch-Mooney (WRM) Correction
The Cross Model is an empirical equation that is used to fit non-Newtonian data (Cross, 1979). this model “describes pseudoplastic flow with asymptotic viscosities at zero (n0) and infinite (*infinity*) shear rates, and no yield stress” (Hackley and Ferraris, 2001). This model is used to fit many types of fluids including dispersions, polymer melts, and polymeric solutions.
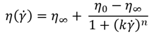
The Carreau-Yasuda Model is another empirical equation used to fit non-Newtonian data (Bird et al., 1987), also “describing pseudoplastic flow with asymptotic viscosities at zero (0) and infinite () shear rates, and with no yield stress” (Hackley and Ferraris, 2001). This model is well suited for fluids that are beginning to shear thin, and can be used to describe emulsions, biopolymer solutions, protein solutions, polymer melts, and polymeric solutions.
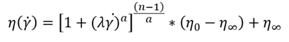
The Carreau-Yasuada model is generalized form of the Power Law Fluid Model, which describes the behavior of a non-Newtonian fluid over the range of shear rates where the fit is performed. The power law model only has two fitting constants which is much simpler than other models that fit non-Newtonian fluids
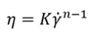
The viscosity of protein formulations is sensitive to changes in temperature. The activation energy of each protein formulation can be calculated from the Arrhenius equation. The activation energy derived from the Arrhenius model can be a useful tool to rank a formulations’ performance.
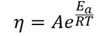
Intrinsic viscosity can be defined as “a measure of a solute’s contribution to the viscosity of a solution”, or more specifically an increase in viscosity as a result of adding an infinitesimal amount of solute to a solvent. To determine the intrinsic viscosity, you must measure the viscosity of your solution at different concentrations and then apply the Huggins and Kraemer equation. The Huggins Equation is an empirical equation used to relate the reduced viscosity of a dilute polymer solution to the concentration of the polymer in solution.
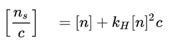
Using an empirical model known as the Mark-Houwink-Sakurada relation, intrinsic viscosity correlates to the size of the macromolecules. This correlation allows you to calculate molecular weight or size (M) can be calculated from the intrinsic viscosity value.
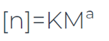
The vast majority of fluids in the world exhibit non-Newtonian behavior. So, knowing how to measure, correct, and handle non-Newtonian rheological data is vital for performing accurate and repeatable experiments and data analysis. One final common correction to note is the Weissenberg-Rabinowitsch-Mooney (WRM) analysis. Some viscometers, including rectangular slit viscometers, apply multiple shear rates across a flow field because of their geometry. Because the shear rate changes within the flow field, both the shear rate and the viscosity must be corrected once data is collected. The WRM correction is an analysis method that can determine the “true shear rate,” using the “apparent shear rate” measured by the viscometer (Macosko, 1994).
Analyzing accurate data is vital for decision making throughout the research and development process. Mathematically modeling your data improves your data analysis and fluid characterization. The constants generated by various model fits have multiple uses from ranking fluid performance to performing calculations that are relevant for your samples. If you want to learn more about model fitting and viscosity measurement corrections, contact us to speak with one of our rheology experts! Or visit our applications note library to read more about the model fittings and how to perform them.
Written by: Eden Reid, RheoSense Senior Marketing and Sales Operations